Литература
Справочная информация
Для учебы
Топографические и обзорно-топографические картыКартографические проекции топографических и обзорно-топографических картОдним из существенных требований, предъявляемых к математической основе топографических и обзорно-топографических карт, является требование сохранения постоянства масштаба в пределах графической точности на всей площади карты. Для указанных карт, являющихся многолистными, можно применять, отдельно для каждого листа или группы листов, любую проекцию, так как искажения в пределах изображения небольшой территории будут практически неощутимыми. До 1917 года для этих карт применялись следующие проекции: — равноугольная коническая проекция Ламберта-Гаусса (карта масштаба 1: 420 000 — десятиверстка, и карты более мелких масштабов) ; — равновеликая псевдоконическая проекция Бонна (карта масштаба 1: 126000 — трехверстка); — многогранная проекция (карты масштабов 1: 21 000 — полуверстка, 1 : 42 000 — верстовка и 1 : 84 000 — двухверстка). После 1917 года многогранная проекция применялась до 1928 года для карт масштабов 1 : 25 000—1 : 200 000. Карты масштабов 1: 500 000 и 1: 1 000000 первоначально составлялись в многогранной конической проекции, разработанной геодезистом Щеткиным. С 1928 года все карты масштабов 1: 10000—1: 500000 составляются в равноугольной поперечно-цилиндрической проекции Гаусса, а карта масштаба 1 : 1 000000 с 1941 года составляется в видоизмененной поликонической проекции, применяемой отдельно для каждого листа.
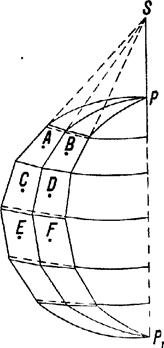
Рис.1 Часть многогранника, середины граней которого касаются эллипсоида Многогранная проекция применялась и в ряде других стран. Например, в Германии до последнего времени в этой проекции составлялись карты масштабов 1:100000 1:200000 1: 300 000. Многогранная проекцияПредставим, что поверхность земного эллипсоида разделена меридианами и параллелями на небольшие трапеции. Вообразим, далее, многогранник, грани которого касаются трапеций в их средних точках А, В, С, D, E, F и т. д. (рис. 43) или проходят через вершины их углов. В первом случае эллипсоид будет заключен в многограннике, а во втором случае — многогранник в эллипсоиде. Если на плоские грани первого или второго многогранника тем или иным путем спроектировать эллипсоидальные трапеции, а затем поверхность многогранника развернуть в плоскость, то в результате получится изображение земной поверхности на плоскости в так называемой мрогогранной проекции. Однако такое определение многогранной проекции не является полным, так как оно не показывает, каким путем изображается поверхность эллипсоида на гранях многогранника, так как каждая проекция характеризуется именно способом изображения одной поверхности на другой. Схему получения изображения в многогранной проекции можно представить и иначе, а именно как результат проектирования каждой трапеции (целого пояса) на поверхность касательного или секущего конуса с последующим развертыванием ее в плоскость. При незначительных размерах трапеций (целых поясов) они изобразятся в этом случае на плоскости практически без каких либо ощутимых искаженней. На многограннике можно изобразить всю земную поверхность (все трапеции, на которые она разделена), однако развернуть многогранник в плоскость без разрывов между отдельными его гранями (трапециями) невозможно.Теоретически
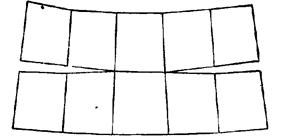
Рис 2. Угловые разрывы при склейке двух поясов трапеций Теоретически возможно, соединить на плоскости колонку трапеций, идущих с юга на север, или пояс трапеций, идущих с запада на восток, но нельзя без разрывов соединить два смежных пояса или две смежные колонки трапеций. На рис. 2 показаны разрывы, возникшие при склейке двух поясов трапеций, а на рис. 3 при склейке девяти трапеций. Величина углового разрыва
Где
Из формулы (38) видно, что величина углового разрыва зависит от размера трапеции и широты
А для трапеций масштаба 1:1000000, с размерами сторон
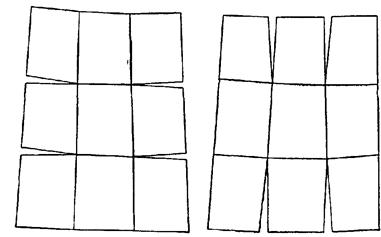
Рис. 3 Угловые разрывы при склейке девяти трапеций. Вид многогранной проекции зависит от способа изображения трапеций на гранях многогранника. Трапеции могут изображаться на плоскости по правилам тех или иных проекций*, например азимутальных, конических, цилиндрических, поликонических. В результате
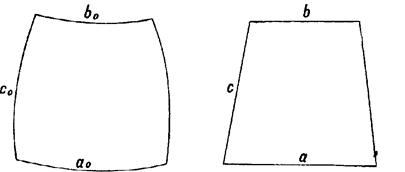
Рис 4 Трапеция на эллипсоиде и на плоскости Будут получаться многогранные азимутальные, конические, цилиндрические, поликонические проекции, которые принято называть их собственными названиями с добавлением слов «применяемая как многогранная», например: «равноугольная коническая проекция, применяемая как многогранная». В более узком смысле слова под многогранной понимают проекцию, применяемую только для топографических карт, которая строится по особому закону. Сущность этой проекции заключается в том, что трапеция, расположенная на поверхности эллипсоида, изображается плоской равнобочной трапецией, стороны которой соответственно равны сторонам трапеции на эллипсоиде. Так, на рис. 4 стороны а0, b0 и с0 трапеции на эллипсоиде соответственно равны сторонам а, b и с плоской трапеции. Исходя из этого, для изображения сторон трапеции на плоскости необходимо вычислить в масштабе карты длины соответствующих дуг меридианов и параллелей, образующих на эллипсоиде трапецию, по формулам
Где Rю и rс — соответственно радиусы южной и северной параллелей трапеции На земном эллипсоиде,
Крайних параллелей трапеции, выраженные в радианной мере, МM — радиус кривизны меридиана для широты средней параллели Трапеции Для построения трапеции на плоскости, кроме размеров ее сторон, необходимо знать еще длину ее диагонали d, которая определяется по формуле
Обычно размеры сторон и диагоналей трапеций при применении многогранной проекции выбирались в готовом виде из таблиц. Хотя эта многогранная проекция по характеру искажений и относится к произвольным, однако она дает неощутимые искажения углов и площадей в пределах листа топографической карты, в связи с чем масштаб остается практически постоянным во всех частях карты.
Топографические и обзорно-топографические карты - 2.5 out of
5
based on
2 votes
|
Материалы по темам:Основи картографії |


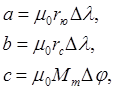 (39)
(39)