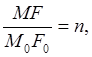Литература
Справочная информация
Для учебы
Теорія перекручувань. Масштаб площіМасштаб площіМасштабом площі в даній точці карти називається відношення площі нескінченно малого еліпса на карті до площі відповідного нескінченно малого кола на земному еліпсоїді. Відомо, що площа еліпса з півосями А і B обчислюється за формулою
а площа за формулою
Позначивши масштаб площі буквою Р і узявши відношення площі еліпса к' площі кругу, будемо мати
Або
З останнього вираження видно, що масштаб площі в даній точці карти дорівнює добуткові масштабів за головними напрямками у цій же точці. Вважаючи головний масштаб карти
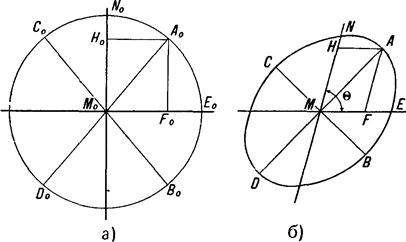
Де А і B-числа відвернені, що виражають собою довжини великої і малої півосей еліпса перекручувань на карті в радіусах нескінченно малого кола на еліпсоїді. Для визначення масштабу площі можна вчинити інакше. Нехай напрямкам меридіана M0N0 і паралелі М0E0 у нескінченно малому колі на еліпсоїді (мал. 12 а) відповідають на карті в еліпсі перекручувань розташовані під кутом у напрямки, MN і ME (мал. 12 б), точкам H0, А0, F0 відповідають точки H, А и F, а напрямкам A0D0 і З0B0 - головні напрямки (осі еліпса) AD і СВ. Тоді масштаб площі можна визначити як відношення площі нескінченно малого паралелограма MHAF до площі нескінченно малого прямокутника M0H0 A0F0, і одержати рівність
Але
Отже,
Тобто: масштаб площі дорівнює добуткові масштабів за меридіаном і паралеллю на синус кута між ними. Отже, для визначення масштабу площі можна користуватися як формулою (4), так і формулою (5).
Мал. 12. Напрямок меридіана і паралелі в нескінченно малому колі на еліпсоїді і відповідному йому еліпсі на карті Знаючи масштаб площі, можна визначити і відносне перекручування площі
Відносне перекручування площ так само, як і відносне перекручування довжин, виражається у відсотках. Так наприклад, якщо р=1,23, те Слід зазначити, що, крім поняття масштабу площі, існує також поняття збільшення масштабу площі, під яким розуміють відношення площі нескінченно малої фігури на карті до площі відповідної нескінченно малої фігури на глобусі, масштаб якого дорівнює головному масштабові карти. Саме це збільшення і характеризує собою перекручування площ. При
Теорія перекручувань. Масштаб площі - 4.0 out of
5
based on
1 vote
|
Материалы по темам:Основи картографії |


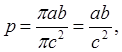
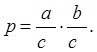
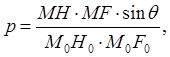
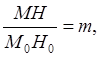 а
а