Литература
Справочная информация
Для учебы
Проекция карты УкраиныПроекция карты Украины масштаба 1: 1 000000Карта Украины масштаба 1: 1 000000 составляется и издается отдельными листами в рамках, имеющих форму трапеций с основаниями в виде дуг окружностей. Верхними и нижними основаниями трапеций служат параллели карты с широтами, кратными 4°. Каждый лист простирается по широте на 4°. Боковыми сторонами трапеций служат меридианы карты с долготами от Гринвича, кратными 6° — южнее 60-й параллели, 12° — между 60-й и 76-й параллелями, 24° — между 76-й и 88-й параллелями. Каждый лист карты в этих поясах соответственно, простирается по долготе на 6, 12 и 24°. Листы, имеющие размеры по долготе 12 и 24°, соответственно считаются сдвоенными и счетверенными. Параллели на, всех листах карты и меридианы на листах, южнее 60-й параллели, проводятся через 1°. Меридианы на сдвоенных листах проводятся через 2° и на счетверенных через 4°. Для карты международного масштаба 1:1000000 принята видоизмененная поликоническая проекция, которая применяется как многогранная, т. е. отдельно для каждого листа. Иначе эта проекция называется проекцией международной миллионной карты. Проекция определяется следующими условиями: — все меридианы — прямые линии; — крайние параллели — дуги окружностей, сохраняющие геодезическую кривизну, т. е. описанные радиусами P = N Ctg , Где N — радиус кривизны первого вертикала земного эллипсоида для данной широты р., взятый в масштабе карты; крайние параллели перпендикулярны к среднему меридиану, т. е. их центры лежат на среднем меридиане; Указанная проекция принята для международной миллионной карты идея о создании которой была выдвинута в 1891 году на V международном географическом конгрессе. —длины сохраняются вдоль крайних параллелей и меридианов с долготами ±2° от среднего меридиана для одинарных листов, ± 4° для сдвоенных и ± 8° для счетверенных листов; —промежуточные параллели делят все меридианы на равные части. Сущность вычисления проекции сводится к определению данных для построения крайних параллелей листа карты. Эти параллели строятся по прямоугольным координатам ряда их точек. За ось X на листе карты (рис. 1) принимают прямую, изображающую средний меридиан, а за ось К—прямую, перпендикулярную к этому меридиану в точке его пересечения с южной параллелью. Пусть ХП — длину дуги меридиана от экватора до северной параллели, взятую в масштабе карты, XS — длину дуги меридиана от экватора до южной параллели, взятую в масштабе карты, H=оlO, Будем иметь H = Xn-Xs-k. (47) В этой формуле значения ХП И XS могут быть выбраны из геодезических или картографических таблиц по аргументу широты K = 0,271 cos2 Где
Рис.1. Оси прямоугольных координат на листе карты масштаба 1:1000000 По этой формуле k получается с точностью до 0,01 мм; для всех листов карты СССР масштаба 1:1000000 он не превышает 0,19 мм. Для определения прямоугольных координат точек пересечения северной параллели с широтой Пусть произвольная точка М, лежащая на северной параллели, имеет географические координаты Длина Длина соответствующей дуги на глобусе— ГN L, или Так как отрезок по параллели на карте, по условию проекции, равен соответствующему отрезку по параллели на глобусе, то, следовательно,
Откуда
Из
Где (49)
Для определения абсциссы хn вначале найдем отрезок Х'N = о1А,
или
Но из формулы (49)
Следовательно,
Или окончательно
Очевидно, что
Точно так же можно определить прямоугольные координаты xs и ys любой точки С, лежащей на южной параллели, по ее географическим координатам
Где
Так как промежуточные параллели проводятся на карте через точки, получаемые делением каждого меридиана на четыре равные части, то прямоугольные координаты х и у любой из этих точек, заданной географическими координатами
Где Вычисление прямоугольных координат произвольных точек в этой проекции может иметь место в том случае, если необходимо нанести на карту геодезические или астрономические пункты по их географическим координатам. Прямоугольные координаты точек для построения картографической сетки обычно даются в таблицах, приложенных к наставлению по составлению карты масштаба 1:1 000000. Проекция карты Украины масштаба 1:1000000 по характеру искажений относится к произвольным. При соединении четырех листов карты, имеющих общую вершину, возникает угловой разрыв. Угловой разрыв
Где
Угловому разрыву Cos При соединении девяти листов (три ряда по три листа) возникает четыре разрыва по меридианам или параллелям. По малости этих разрывов практически можно склеивать как четыре листа, имеющих общую вершину углов рамок, так и девять листов (три ряда по три листа). В пределах одного пояса или одной колонны допустимо склеивание любого числа листов. Для определения масштаба по любому меридиану может быть применена приближенная формула: M= 1 +0,0001523 (Lº2 - 4°) cos2 Ее обоснование дано в учебнике проф. М. Д. Соловьева «Картографические проекции» (Геодезиздат, М., 1946) на стр. 335—336. Исследование формулы показывает, что изменение масштаба по меридиану практически не ощущается. Так, при широте <pm, равной 55°, для крайних меридианов (при L°= ± 3°) M= 1,00025 Или υM= 0,025°/о, Что при длине стороны в 40 см соответствует 0,1 мм. Для среднего меридиана (при M = 0,99980, или υM = 0,0200, что при длине стороны в 40 см составит 0,08 мм. Длины по промежуточным параллелям искажаются меньше, чем по крайним меридианам. Поэтому можно считать, что во всех частях листа карты масштаб остается практически постоянным. Построение картографической сетки для каждого листа карты производится посредством координатографа, а при его отсутствии — с помощью металлической масштабной линейки и штангенциркуля; линейка должна иметь такую длину, чтобы по ней можно было измерить диагональ листа. В таблицах, приложенных к наставлению по составлению карты масштаба 1:1000 000, даны прямоугольные координаты точек для построения северной и южной параллелей всех листов карты Украины. За начало координат для каждой крайней параллели листа взята точка ее пересечения со средним меридианом. За ось X принят средний меридиан, а за ось Y—линия, перпендикулярная к среднему меридиану в начале координат. Таким образом, каждый лист карты имеет два начала координат и две оси Y (для северной и южной параллелей). В таблицах приведены координаты точек, расположенных восточнее среднего меридиана. Соответствующие им точки, расположенные западнее среднего меридиана, будут иметь те же абсолютные значения координат, но ординаты их будут отрицательными.
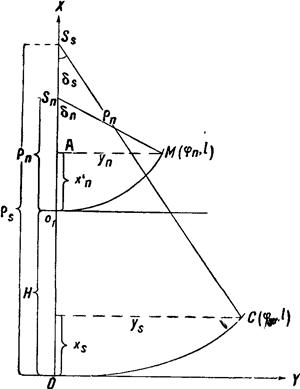
Рис.2 Построение картографической сетки листа карты масштаба 1:10000000 При построении картографической сетки посредством координатографа для приведения координат точек северной и южной параллелей листа карты к одному началу и получения положительного значения всех ординат необходимо к абсциссам точек северной параллели прибавить значение Оо1=Н (рис. 2), которое дается в таблице, а все ординаты увеличить на величину, несколько большую значения ординаты юго-восточной вершины угла рамки листа. При построении картографической сетки с помощью линейки и штангенциркуля нет надобности в приведении координат точек параллелей к одному началу. Нанесение сетки в последнем случае начинается с построения прямоугольника, боковая сторона которого равна длине среднего меридиана Оо1, я верхняя и нижняя стороны равны удвоенному значению ординаты уs вершины одного из углов при южной стороне рамки листа карты. Затем верхнюю и нижнюю стороны прямоугольника делят пополам и, соединив точки деления прямой линией, получают средний меридиан карты. Дальше наносят точки с координатами х1, у1;х2, у2, и т. д., принимая за ось Y для северной стороны рамки верхнюю, а для южной нижнюю Рис. 58. Построение картографической стороны прямоугольника. После сетки листа карты масштаба 1:1000000 того как крайние параллели и Средний меридиан нанесены, по линейке через соответствующие точки крайних параллелей проводятся остальные меридианы. Промежуточные параллели проводятся через точки, полученные делением каждого меридиана на четыре равные части. Контролем правильности построения картографической сетки служат: — равенство диагоналей рамки листа и соответствие их длин табличным данным; — равенство отрезков одной и той же параллели между меридианами; — равенство отрезков одного и того же меридиана, заключенных между параллелями; — соответствие сторон рамки листа карты размерам, указанным в таблице, приложенной к наставлению по составлению карты масштаба 1:1000000; в этой таблице даны размеры хорд, стягивающих дуги северной и южной параллелей, длины крайних меридианов и диагоналей рамок листов по каждому поясу. После проверки сетки крайние параллели и меридианы делятся на отрезки через 5'.
Проекция карты Украины - 2.5 out of
5
based on
2 votes
|
Материалы по темам:Основи картографії |


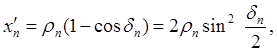 ,
,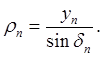
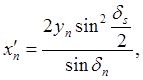
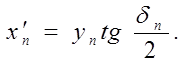 (50)
(50)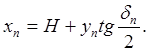 (51)
(51)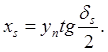 (52)
(52)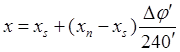 (54)
(54)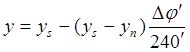 (55)
(55)