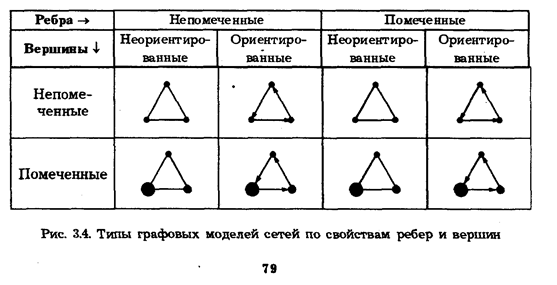
Сетевой анализ

 Географические сети

Важным объектом исследований в географии являются различные Географические сети, представляющие собой совокупности линейных фрагментов природного (например, речные, орографические, тектонические) и антропогенного (например, дорожные, электрические, коммуникационные) характера. В общем случае в понятие "географическая сеть" включаются все пространственные (территориальные) связи и отношения, существенные для изучения пространственной организации природных и социально-экономических систем. В этом случае географическая реальность может быть представлена в виде суперпозиции (объединения, наложение) большого количества разнообразных пространственных отношений и связей (транспортных, технологических, экологических, миграционных, информационных и др.) между различными геообъектами (населенными пунктами, предприятиями, административными и экономическими районами, экосистемами и др.). При этом географичность данных отношений состоит в том, что в указанную суперпозицию всегда включается отношение взаимного размещения, которое и придает всему комплексу территориальный, географический характер.

Целью изучения географических сетей является выявление закономерностей их строения, формирования и развития, а также мониторинг, оптимизация и управление (например, в случае транспортных и коммуникационных сетей). ГИС-технология обеспечивает возможность компьютерного представления, моделирования и анализа, сколь угодно больших по числу вершин и ребер сетевых объектов, в сочетании с автоматизированным тематическим картографированием, интерактивным редактированием и визуализацией (включая мультимедиа) соответствующих сетевых моделей.

Модели и алгоритмы сетевого анализа

В моделировании и анализе географических сетей широко применяются методы теории графов. Как известно, любое картографическое изображение территориальных отношений содержит метрические и топологические атрибуты. Графовые модели акцентируют внимание именно на топологические свойства сетей: порядок соединения вершин, наличие циклов, степень связности и др.

Реальные территориальные отношения и связи можно формализовать и изобразить в виде многомерных графов-картосхем. Однако методика анализа таких графов еще недостаточно разработана. Поэтому при изучении географических сетей чаще всего используются относительно простые графовые модели, методика анализа которых разработана до уровня алгоритмов и программ.

Если в качестве свойств графов рассматривать Помеченность вершин, а также помеченность и Направленность ребер, то можно выделить 8 типов графовых моделей сетей (Рис. 3.4). (Помеченным называется граф, ребрам и/или вершинам которого приписано значение некоторого признака - числового, порядкового, классификационного). Рассмотрим кратко основные типы выделенных графовых моделей:

1. Непомеченные неориентированные графы. С помощью этого типа

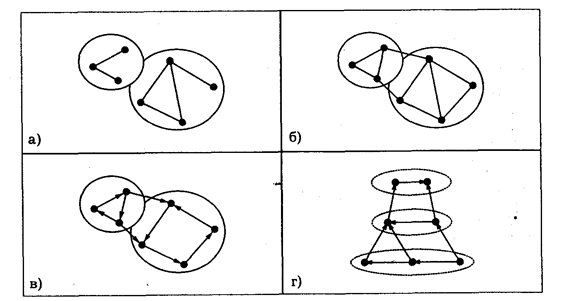
Графовых моделей изучаются территориальные связи и отношения, для которых не известны (или не важны) интенсивность и направление: коммуникационные сети и сообщения (в оба конца), производственные связи, маятниковые миграционные потоки и т. п. Анализ таких графов используется при решении следующих задач:

— исследование связности графа: выявление несвязных подграфов (Рис. 3.5а), критических вершин и ребер (т. е. таких, при удалении которых граф перестает быть связным);

— общая характеристика структуры и формы графа с помощью различных показателей;

— оценка вершин графа по их положению в структуре графа;

— нахождение максимальных полных подграфов (клик) и анализ структуры их соединения в исходном графе (Рис. 3.5б);

— поиск кратчайших путей между вершинами графа, решение оптимизационных задач (задача "коммивояжера" и т. п.);

— преобразование (генерализация) исходного графа в более простой, удобный для анализа и картографирования вид.

Моделирование и анализ рассмотренных графов представляет собой быстро развивающийся раздел комбинаторики, имеющий приложения в различных областях науки и техники. Разработаны и разрабатываются специальные алгоритмические языки и пакеты прикладных

Рис. 3.5. Способы кластеризации графов;

А) изолированные подграфы; б) клики (максимально связные подграфы); В) сильно связные компоненты орграфа; г) слои поточного иерархического графа программ для представления в ЭВМ и анализа графов, в том числе в ГИС.

II. Помеченные неориентированные графы. Этот тип графовых моделей целесообразно использовать в случае, когда известна интенсивность территориальных связей между геообъектами, измеренная в числовой или порядковой шкале. Ключевыми понятиями для анализа помеченных (по ребрам) неориентированных графов являются понятия порога и Устойчивого разбиения. Устойчивое разбиение, например, можно рассматривать как оптимальное расчленение (районирование) географической сети по данному виду связей.

Основные алгоритмы анализа помеченных неориентированных графов следующие: 1) алгоритм получения пороговых матриц смежности вершин графа при различных значениях порога; 2) алгоритм подсчета несвязных компонент графа, задаваемого соответствующей пороговой матрицей.

III. Непомеченные ориентированные графы. Изучая сети, географ иногда располагает информацией лишь о Направлении связей между геообъектами, а их интенсивность ему не известна (или не важна в контексте исследования). В этом случае в качестве моделей географических сетей используются непомеченные ориентированные графы - Орграфы. Для географических приложений важны такие понятия теории орграфов, как Сильно связная компонента и Поточная иерархическая структура.

В географическом аспекте сильно связные компоненты можно рассматривать как функциональные районы, а процесс их выделения - как функциональное районирование географической сети (Рис. 3.5в).

Поточная иерархическая структура - это такое представление орграфа, при котором: 1) вершины разбиты на упорядоченные группы (иерархические слои); 2) вершины, находящиеся в одном иерархическом слое, могут иметь связи только между собой и с вершинами более высоких иерархических слоев (Рис. 3.5г). В географическом плане представление и анализ ориентированных графов в виде поточных иерархических структур дает возможность решить следующие задачи: 1) определить общую иерархическую структуру подчинения геообъектов по данному виду связей (например, населенных пунктов по миграционным связям); 2) оценить значение каждого геообъекта в иерархической структуре территориальных связей (например, ландшафта определенного таксономического ранга); 3) осуществить иерархическое районирование географической сети (например, сети поселений различного ранга по степени миграционной привлекательности).

Алгоритм сокращения поточной иерархической структуры орграфа, являющийся основой иерархического районирования, представляет собой циклическую процедуру поиска максимального элемента в строках матрицы интенсивности связей и не предполагает использования специального программного обеспечения.

IV. Помеченные ориентированные графы. Графовые модели этого типа используются в случае, когда известны интенсивность связей между геообъектами и их направление. Методика анализа помеченных ориентированных графов содержит в качестве этапов нахождение пороговых матриц для различных значений порога и подсчет для каждой из них числа сильно связных компонент, интерпретируемых в качестве функциональных районов.