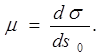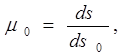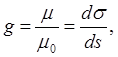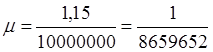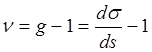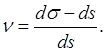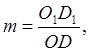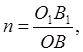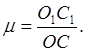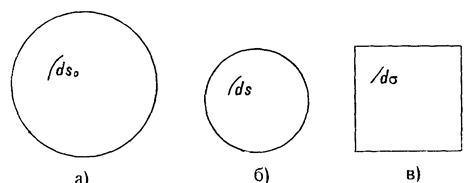
Головний і приватний масштаби карт

Головний і приватний масштаби карти. Масштаби по меридіану і паралелі

Під масштабом у загальному значенні цього слова розуміють ступінь зменшення або збільшення зображення. Під масштабом плану розуміють ступінь зменшення ліній плану стосовно відповідних горизонтальних додатків тих же ліній на місцевості. Масштаб плану практично залишається постійним для всіх його частин, тому що невеликі ділянки Землі, зображувані на плані, із припустимою погрішністю приймаються за плоскі.

На відміну від масштабу плану масштаб на карті є величиною перемінної, тому що карти складаються на всю поверхню Землі або на значні її ділянки, що неможливо прийняти за плоскі.

Для простоти міркувань при зображенні земної поверхні на площині уявимо, що земна поверхня спочатку зображена на кулі визначеного розміру (тобто представлена на глобусі), а потім з його поверхні тим або іншим способом перенесена на площину. При такому способі зображення масштаб глобуса, що служив підставою для побудови карти, називається головним, або загальним, масштабом карти. Інакше це можна сформулювати так: головний, або загальний, масштаб карти являє собою ступінь зменшення земної кулі або еліпсоїда перед наступним зображенням його на площині. Головний масштаб карти звичайно пишеться внизу, під південною стороною рамки карти. Як буде показано нижче, головний масштаб карти мають тільки окремі її точки і лінії, що називаються точками і лініями нульових перекручувань.

Масштаб карти змінюється не тільки при переході від однієї її точки до іншої, але й в одній точці при зміні напрямку. Тому в математичній картографії поряд з головним масштабом карти вводиться поняття приватного масштабу. Приватним масштабом у даній точці карти за даним напрямком називається відношення нескінченно малого відрізка на карті до відповідного нескінченно малого відрізка на поверхні еліпсоїда або кулі.

Для визначення залежності приватного масштабу від головного введемо позначення:

Ds0-нескінченно малий відрізок на земному еліпсоїді (мал. 9а);

Ds і D - відповідні йому нескінченно малі відрізки на глобусі (мал. 96) і на карті (мал. 9 в);

-головний, або загальний, масштаб карти;

- приватний масштаб.

Відповідно до визначення будемо мати

Визначимо звідси відношення g частки масштабу до головного

Відкіля

Відношення приватного масштабу до головного називається збільшенням довжин, або просто збільшенням.

Мал. 9 Нескінченно малий відрізок: а) на земному еліпсоїді, б) на глобусі, в) на карті

Як видно з формул (1) і (2), збільшення довжин виражає собою відношення нескінченно малого відрізка на карті до відповідного нескінченно малого відрізка на глобусі і характеризує зміну приватного масштабу, представляючи собою множник, на який треба помножити головний масштаб , щоб одержати приватний масштаб .

Приклад. Відомо, що на карті масштабу 1:10000000, (при =1:10000000) збільшення довжин у даній точці по даному напрямку g=1,15. Визначити, чому дорівнює приватний масштаб у даній точці по даному напрямку.

Рішення.

Очевидно, що чим ближче до одиниці збільшення довжин, тим менше перекручування має зображення на карті.

Позначивши відхилення збільшення довжин від одиниці буквою v, будемо мати

Відкіля

Аналізуючи отримане вираження (3), бачимо, що чисельник у правій частині рівності і являє собою абсолютне перекручування довжини відрізка ds при перенесенні його з глобуса на карту, а в цілому права частина рівності виражає відносне перекручування довжини того ж відрізка. Таким чином, відхилення збільшення від одиниці v являє собою відносне перекручування довжин. Значення v звичайно виражають у відсотках, наприклад, якщо g=1,12, то v=g-1=0,12, або v=12%.

При вивченні перекручувань тієї або іншої проекції викликає інтерес не головний і не приватні масштаби карти, а відношення приватного масштабу до головного, тобто збільшення довжин, що характеризує перекручування довжин ліній при перенесенні їхній із глобуса на карту.

У математичній картографії для полегшення викладу про перекручування головний масштаб карти звичайно приймається рівним одиниці, тобто вважається, що земний еліпсоїд на карті зображується в натуральну величину.

Щоб після обчислення даних для побудови картографічної сітки за умови Перейти до побудови сітки в необхідному головному масштабі карти, необхідно зменшити всі лінійні розміри згідно дійсному головному масштабові карти. При буде справедлива рівність . З огляду на зазначену умову ( ), в подальшому викладі при дослідженні лінійних перекручувань під масштабом на карті фактично буде розумітися не приватний масштаб карти, а збільшення довжин g, тобто відношення нескінченно малого відрізка на карті до відповідного нескінченно малого відрізка на глобусі, масштаб якого дорівнює головному масштабові карти. Під масштабом по меридіану (паралелі) буде розумітися відношення нескінченно малого відрізка меридіана (паралелі) на карті до відповідного нескінченно малого відрізка меридіана (паралелі) на глобусі.

З усіх приватних масштабів, що розглядаються в математичній картографії, найбільше значення мають масштаби по меридіану і паралелі, тому що меридіани і паралелі є невід'ємною основою всякої карти. Меридіани і паралелі на поверхні еліпсоїда завжди перетинаються під прямим кутом. На площині ж меридіани і паралелі можуть перетинатися під кутом, не рівним 90°.

У математичній картографії вводяться наступні позначення:

M — масштаб по меридіану;

N - масштаб по паралелі;

— кут між меридіаном і паралеллю на площині;

— азимут будь-якого напрямку ОС на поверхні еліпсоїда (мал. 10 а);

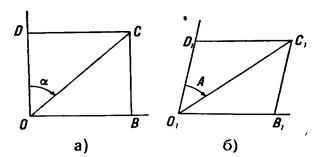
А — азимут відповідного напрямку ПРО1С1 на площині (мал. 10 б).

Якщо OD, ОВ і ОС являють собою нескінченно малі відрізки відповідно по меридіану, паралелі

Мал. 10. Азимут а на еліпсоїді й азимут А на карті

Довільному напрямкові на еліпсоїді, а на площині їм відповідають нескінченно малі відрізки O1D1, O1B1 і ПРО1С1, те