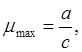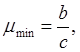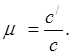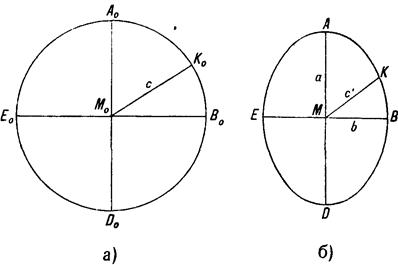
Теорія перекручувань. Еліпс перекручувань

Еліпс перекручувань. Головні напрямки і масштаби по них.

У докладних курсах математичної картографії доводиться, що нескінченно мале коло, взяте на глобусі, при перенесенні його на площину будь-яким способом зображується нескінченно малим еліпсом. В окремих випадках нескінченно мале коло може відобразитися на площині нескінченно малим колом або нескінченно малим відрізком прямої. Це, однак, не суперечить загальному положенню, тому що коло і відрізок прямої являють собою окремі випадки еліпса, у якого в першому випадку велика вісь дорівнює малій, а в другому випадку — мала вісь дорівнює нулю.

Нескінченно малий еліпс на карті (площині), що відповідає нескінченно малому колу на глобусі, називається еліпсом перекручувань. Назву еліпса перекручувань він носить тому, що його розміри і форма цілком характеризують перекручування довжин, кутів і площ фігур при перенесенні їх із глобуса на карту.

Нехай нескінченно мале коло на глобусі з центром у точці М0 і радіусом З (мал. 11 а) відповідає на карті еліпсові перекручувань з центром у точці М и півосями А і B (мал. 11 б) і нехай напрямкам півосей еліпса перекручувань МА і MB відповідають на глобусі напрямки двох взаємо-перпендикулярних напівдіаметрів кола М0А0 і M0В0.

У докладних курсах математичної картографії доводиться, що головним осям еліпса перекручувань на площині обов'язково відповідають два взаємо-перпендикулярних діаметри відповідного нескінченно малого кола на сфері.

Мал. 11. Нескінченно мале коло на глобусі і відповідний йому еліпс

Перекручувань на карті

Увівши позначення

A0M0 = з, МА = А, МВ = b, МК = с',

Де До-довільна точка на еліпсі, одержимо масштаби при точці М за напрямками MA, MK і MB у вигляді

Позначивши масштаб у будь-якому напрямку буквою , для зазначених трьох напрямків будемо мати

і

Позначивши масштаб у будь-якому напрямку буквою , для зазначених трьох напрямків будемо мати

Приймаючи радіус з нескінченно малого кола на глобусі рівним одиниці, остаточно одержимо

Де А, b і С' — абстрактні числа, що виражають собою довжини великої і малої півосей еліпса перекручувань і радіуса-вектора довільної точки в радіусах відповідного нескінченно малого кола на глобусі.

Очевидно, що в будь-якій точці карти масштаб буде мати найбільше значення ( ) у напрямку великої осі (напрямку МА і МD) і найменше значення ( ) у напрямку малої осі (напрямку MB і ME) еліпса перекручувань, що між собою взаємо перпендикулярні. Такі два взаємо-перпендикулярних напрямки в будь-якій точці карти, що мають найбільший і найменший масштаби, називаються головними напрямками.

З визначення постає, що масштаб за одним із головних напрямків дорівнює великої півосі А еліпса перекручувань, а за іншим напрямком його малої півосі B вираженим у радіусах відповідного нескінченно малого кола на глобусі. Якщо в даній точці карти А= 1,5, B=1,2, то це означає, що масштаб за напрямком великої півосі еліпса перекручувань у 1,5 рази, а по напрямком його малої півосі в 1,2 рази крупніше головного масштабу карти (масштабу глобуса). Так як меридіани і паралелі на глобусі у всіх його точках перетинаються під прямими кутами, то вони будуть головними напрямками на карті лише в тих її точках, де вони перетинаються також під прямими кутами; у тих же точках карти, де меридіани і паралелі перетинаються під гострими або тупими кутами, вони головними напрямками бути не можуть.