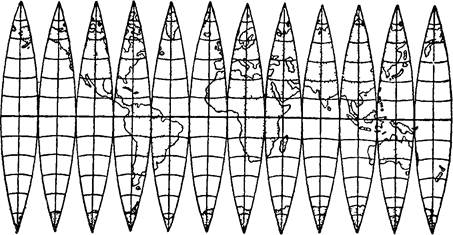
Загальні відомості про геодезичну і математичну основу карт

Геодезична і математична основа карт. Загальні відомості

Сферичну поверхню неможливо розгорнути в площину без складок і розривів, тобто без перекручувань. Тому значна ділянка земної поверхні або вся земна поверхня може бути зображена зі збереженням подоби всіх обрисів тільки на поверхні кулі, оскільки форма Землі близька до кулі. Куля з ображеною на ній поверхнею Землі зветься глобусом.

Зображення земної поверхні, представленої на глобусі, характеризується наступними цінними властивостями:

Кути між напрямками на глобусі дорівнюють кутам між відповідними напрямками на земній поверхні;

Відношення довжин ліній на глобусі до відповідних довжин ліній на земній поверхні зберігається постійним, тобто масштаб зображення однаковий на всій поверхні глобуса;

Відношення площ на глобусі до відповідних площ на земній поверхні має постійне значення.

Однак глобуси при всіх їхніх позитивних якостях є громіздкими і користування ними пов'язане з великими незручностями. Так, наприклад, глобус у масштабі 1:1000000 у випадку, якби він був виготовлений, мав би діаметр близько 13 м. Тому глобуси виготовляють в основному для навчальних цілей і, як правило, у дрібних масштабах. Звичайно ж, незважаючи на неминучість перекручувань, звертаються до зображення земної поверхні на площині — до складання карти, що є портативною, зручною для збереження і користування.

При зображенні земної поверхні на площині порушуються або усі вищевказані властивості її зображення, представленого на глобусі, або велика частина них. Збереження одних, певних властивостей може бути здійснено тільки за рахунок порушення інших.

Для наочної ілюстрації того, як виникають на картах перекручування, уявімо собі поверхню глобуса, розрізану по меридіанах на зони — досить вузькі, щоб кожну з них без відчутних перекручувань можна було розгорнути в площину. При з'єднанні цих зон на площині так, як показано на мал. 4, виходять розриви за меридіанами та паралелями.

Мал 4 Поверхня глобуса, розрізана за меридіанами та паралелями на зони.

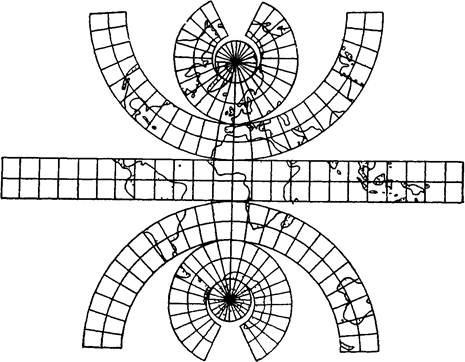
Мал 5 Поверхня глобуса, розрізана по меридіанам на зони

Якщо поверхня глобуса розрізати на досить вузькі пояси по паралелях, то при їхньому з'єднанні на площині так, як показано на мал. 5, виходять розриви по паралелях.

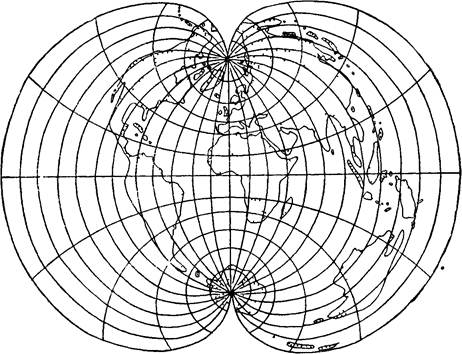
Мал 5. Поверхня глобуса, розрізана по паралелям на пояси

Для того щоб із сукупності таких зон або поясів одержати безперервне і разом з тим однозначне зображення — географічну карту, необхідно в місцях розривів зробити їхнє розтягання. Це і призведе до перекручування зображення, що малося на зонах або поясах (мал. 6 і 7).

Мал. 6 Карта світу, отримана розтяганням зон, показаних на мал. 4

Мал 7 Карта світу, отримана розтяганням поясів, показаних на мал. 5

Порівнюючи зображення материків, островів, морів на глобусі і на карті, можна бачити усі види перекручувань, властиві географічній карті, а саме перекручування довжин, перекручування площ, перекручування кутів і перекручування форм полягає в тому, що фігури на карті не подібні відповідним фігурам на глобусі. Відомо, що фігури, розташовані на площині, є подібними, якщо в них рівні відповідні кути. Однак, якщо одна з фігур знаходиться на площині, а інша на поверхні кулі, то це положення залишається в силі тільки для нескінченно малих фігур. Тому обрису (форма) материків, островів, морів тощо при перенесенні їх із глобуса на карту навіть при збереженні рівності відповідних кутів усе рівно будуть зображені з перекручуванням. Звідси випливає, що перекручування форм на карті рівнозначно перекручуванню кутів на ній тільки для нескінченно малих фігур.

При різних способах зображення земної поверхні на карті неминуче будуть спотворюватися довжини і, крім того, кути або площі в одних випадках, кути і площі одночасно — в інших. Величини перекручувань, що можуть бути значними або мало відчутними, залежать від розміру території, що картографується, і способу побудови зображення.

Для того, щоб на карті можна було робити різні виміри, пов'язані з визначенням відстаней, площ, кутів і напрямків, до картографічного зображення висуваються наступні вимоги:

Зображення повинне бути підлегле визначеному математичному законові, що дозволяє визначати в будь-якій точці карти масштаб (перекручування довжин), перекручування площ, кутові перекручування і перекручування форм;

Перекручування території, що картографується, повинні бути, можливо меншими;

Зображення повинне бути безперервне, суцільне, тобто без розривів;

Зображення повинне бути однозначним: кожній точці на земній поверхні повинна відповідати одна єдина точка на карті.

З метою виконання цих вимог усяка географічна карта будується на визначеній геодезичній і математичній основі.

Геодезична основа визначає перехід від фізичної поверхні Землі до умовної математичної поверхні (поверхні еліпсоїда) і забезпечує правильне положення зображуваних на карті географічних об'єктів відповідно їх широті, довготі і висоті.

Фізична поверхня Землі є складною і неправильною, тому при картографуванні, перш ніж переходити до плоского зображення, її проектують на умовну (допоміжну), більш просту, математичну поверхню (поверхня еліпсоїда), найбільш близьку до фігури Землі в цілому. Геодезична основа карти і залежить насамперед від характеру і розмірів цієї умовної математичної поверхні, а також від її орієнтування в тілі Землі.

До геодезичної основи належать опорні пункти, закріплені на місцевості точки, положення яких на земній поверхні або на умовній математичній поверхні (поверхні еліпсоїда) визначено за допомогою координат. Опорні пункти, якщо, наприклад, відомі їхня широта і довгота, дозволяють при складанні карти правильно розташовувати елементи її змісту щодо ліній меридіанів і паралелей.

До математичної основи належать масштаб, картографічна проекція і система розграфлення карти на аркуші. Масштаб визначає ступінь зменшення зображення місцевості на карті і ступінь деталізації при побудові цього зображення.

Картографічна проекція обумовлює перехід від умовної математичної поверхні (поверхні еліпсоїда) до площини і дає закон розподілу виникаючих при цьому перекручувань. Система розграфлення визначає кількість і величину аркушів, на які поділяється та або інша карта.